The Theory of Causal Fermion Systems

In daily life we experience space and objects therein. These objects are typically described by densities, and integrating these densities over space gives particle numbers, charges, the total energy, etc. In mathematical terms, the densities are usually described as the normal components of vector fields on a Cauchy surface, and conservation laws express that the values of these integrals do not depend on the choice of the Cauchy surface, i.e.

\[ \int_{\scrN_1} J_k \nu^k\: d\mu_{\scrN_1}(x) = \int_{\scrN_2} J_k \nu^k\: d\mu_{\scrN_2}(x) \:, \]

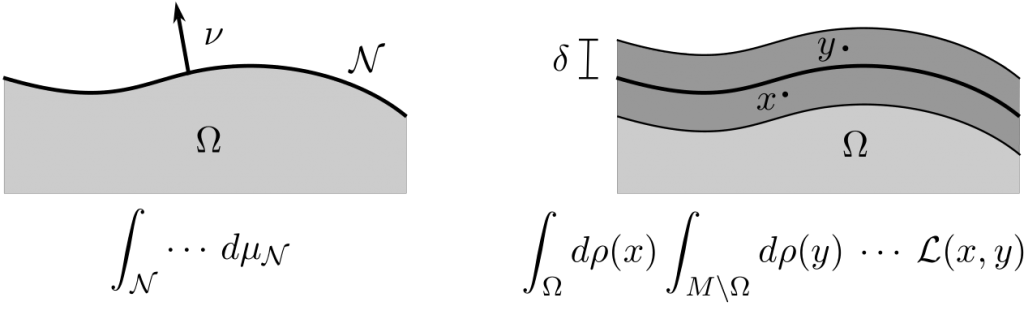
where $\scrN_1$ and $\scrN_2$ are two Cauchy surfaces, $\nu$ is the future-directed normal, and $d\mu_{\scrN_{1/2}}$ is the induced volume measure (see the left of the figure below).

In the setting of causal fermion systems, surface integrals are undefined. Instead, one considers so-called surface layer integrals, as we now explain. In general terms, a surface layer integral is a double integral of the form

\[ \int_\Omega \bigg( \int_{M \setminus \Omega} \cdots\: \L(x,y)\: d\rho(y) \bigg)\, d\rho(x) \:, \]

where one variable is integrated over a subset $\Omega \subset M$, and the other variable is integrated over the complement of $\Omega$. In order to explain the basic idea, we make the assumption that the Lagrangian is of short range in the following sense. We let $d \in C^0(M \times M, \R^+_0)$ be a distance function on $M$. The assumption of short range means that $\L$ vanishes on distances larger than $\delta$, i.e.

\[ d(x,y) > \delta \quad \Longrightarrow \quad \L(x,y) = 0 \:. \]

Then the above surface layer integral only involves pairs $(x,y)$ of distance at most $\delta$, where $x$ is in $\Omega$ and $y$ is in the complement $M \setminus \Omega$. Thus the integral only involves points in a layer around the boundary of $\Omega$ of width $\delta$. Therefore, a surface layer integral can be regarded as an approximation of a surface integral on the length scale $\delta$. This is illustrated on the right of the next figure.