The Theory of Causal Fermion Systems
Spin Spaces and Physical Wave Functions
Prerequisites
Continue Reading
Related Topics
Spin Spaces and Physical Wave Functions
The Spin Spaces
The causal action principle depends crucially on the eigenvalues of the operator product $xy$ with $x,y \in \F$. For computing these eigenvalues, it is convenient not to consider this operator product on the (possibly infinite-dimensional) Hilbert space $\H$, but instead to restrict attention to a finite-dimensional subspace of $\H$, chosen such that the operator product vanishes on the orthogonal complement of this subspace. This construction leads us to the spin spaces, which we now introduce. For every $x \in \F$ we define the spin space $S_x$ by $S_x = x(\H)$; it is a subspace of $\H$ of dimension at most $2n$ (for clarity, the spin space is often also denoted by $S_xM$). On the spin space one introduces the spin inner product $\Sl\! .|. \Sr_x$ by
\[ \Sl u |\; v \Sr_x : S_x \times S_x \longrightarrow \C\:,\qquad \Sl u |\: v \Sr_x = -\la u |\: x v \ra_\H \:. \]
The spin space $(S_x, \Sl .|. \Sr_x)$ is an indefinite inner product space of signature $(p,q)$ with $p,q \leq n$.
In this way, to every spacetime point $x \in M$ we associate a complex vector space. This structure resembles a vector bundle. However, as a major difference to a bundle structure, here all the spin spaces are subspaces of one larger vector space, the Hilbert space $\H$. This is illustrated in the following figure:

The Physical Wave Functions
A wave function $\psi$ is a mapping which to every spacetime point $x \in M$ associates a vector $\psi(x) \in S_x$ of the corresponding spin space. The vectors in the Hilbert space can be represented by specific wave functions, referred to as the physical wave functions: Given $u \in \H$, the corresponding physical wave function $\psi^u(x)$ evaluated at $x \in M$ is obtained by taking the orthogonal projecton on the spin space $S_x$,
\[ \psi^u \::\: M \longrightarrow \H \:,\qquad \psi^u(x) = \pi_x u \in S_x \]
(where $\pi_x : \H \rightarrow S_x \subset \H$ is the orthogonal projection). This construction is illustrated in the following figure:
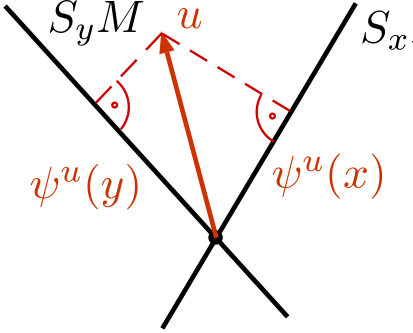
The resulting ensemble of physical wave functions is the reason for the notion fermion in “causal fermion system.”
The Topological Spinor Bundle
Taking the collection of all spin spaces,
\[ SM := \bigcup_{x \in M} S_x \:, \]
gives a structure similar to a vector bundle. The only difference is that the dimension of the fibres may depend on $x$. The physical wave functions give distinguished sections of this bundle. No smoothness assumptions are required. The topology of this so-called topological spinor bundles and the connection to the topological spin assumption of spin manifolds are worked out in [topology14].
→ The fermionic projector
→ The Euler-Lagrange equations

Felix Finster
Author