The Theory of Causal Fermion Systems
The Fermionic Projector
Prerequisites
Continue Reading
Related Topics
The Fermionic Projector
The Kernel of the Fermionic Projector
The kernel of the fermionic projector defined by
\[ P(x,y) = \pi_x \,y|_{S_y} \::\: S_y \longrightarrow S_x \]
is a mapping from one spin space to another. It gives relations between different spacetime points $x, y \in M$. It can be decomposed into physical wave functions. Indeed, choosing an orthonormal basis $(e_i)$ of $\H$,
\[ P(x,y) \, \phi = \pi_x y|_{S_y} \,\phi = \sum_i \pi_x e_i \: \la e_i |\; y\,\phi \ra_\H = -\sum_i \psi^{e_i}(x) \: \Sl \psi^{e_i}(y) |\; \phi \Sr_y \:. \]
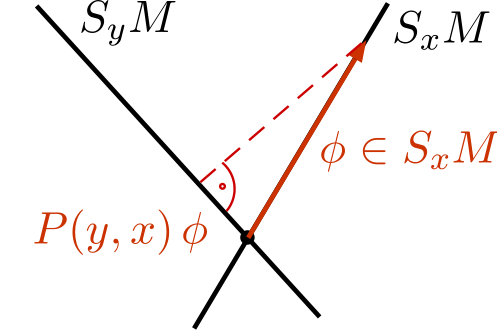
The kernel of the fermionic projector plays a central role for several reasons:
- The Lagrangian and the constraints can be expressed in terms of $P(x,y)$. This can be understood from the fact that the operators $xy : \H \rightarrow \H$ and $\pi_y xy|_{S_y} : S_y \rightarrow S_y$ have the same eigenvalues and algebraic multiplicities, up to zeros in the spectrum. The latter operator can be expressed in terms of the kernel of the fermionic projector by \[ \pi_y \, x y|_{S_y} = \pi_y \, x\, \pi_x \, y|_{S_y} = P(y,x)\, P(x,y) \::\: S_y \rightarrow S_y \:. \] The combination $P(y,x)\, P(y,x)$ is also referred to as the closed chain.
- Being a mapping from one spin space to another, it gives relations between different spacetime points. In this way, it carries all the information on the causal and geometric structure of spacetime.
- Being composed of all the physical wave functions, it carries all the information on the distribution of matter in spacetime.
The Fermionic Projector as an Operator on Wave Functions
The kernel of the fermionic projector can be taken as the integral kernel of a corresponding integral operator $P$,
\[ (P \psi)(x) := \int_M P(x,y)\: \psi(y)\: d\rho(y) \:, \]
referred to as the fermionic projector. Here $\psi$ is a wave function (i.e. a mapping from $M$ to $\H$ with the property that $\psi(x) \in S_x$ for all $x \in M$; in other words, $\psi$ is a section of the topological spinor bundle). The fermionic projector is a symmetric operator if the wave functions are endowed with the indefinite inner product
$\displaystyle \bra \psi | \phi \ket = \int_M \Sl \psi(x) | \phi(x) \Sr_x \: d\rho(x) \:.$
This indefinite inner product can be given the structure of a Krein space with the topology induced by the scalar product
\[ \la\!\la \psi | \phi \ra\!\ra = \int_M \la \psi(x) |\, |x|\, \phi(x) \ra_\H \:d\rho(x) \:. \]
(where $|x|$ is the absolute value of the operator $x$). The fermionic projector is an in general unbounded, densely defined linear operator on this Krein space. The operator $(-P)$ is positive in the sense that for all $\psi$ in the domain,
$\bra \psi | (-P) \psi \ket \geq 0 \:.$

Felix Finster
Author